The Triangle Puzzle

Scroll Down For The Answer

The reason that people sometimes find this puzzling is because they start off making an assumption. Often they don't even realize they have made this assumption. The assumption is that we are comparing two triangles, and that they each have the same area. Certainly a quick inspection - helped by the grid - is that the 'triangles' are 13 squares across, and five squares high, and they kind of look the same.

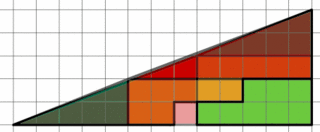
In fact the top triangle is not a triangle at all, it is a tetrahedron. If you look closely along the line of the hypotenuse (the diagonal), you will see that it is not quite straight, it is slightly concave. Why? Well, the dark green triangle is 5 squares across, and 2 squares high. The red triangle is 3 squares high, and should be 7.5 squares across for the hypotenuse to have the same angle to the horizontal. In fact the red triangle is 8 squares across, and the angle of the hypotenuse is slightly shallower that that of the green triangle. Which is why the hypotenuse is not a straight line, when you look closely. The bottom 'triangle' is not a triangle either, it is also a tetrahedron, but now the hypotenuse is slightly convex, since the position of the red and green triangles is now reversed.

Here is an image of the two triangles superimposed, which shows the difference in the two hypotenuse...